Зачёт

Математический анализ.

1.Множества.

1) Множество, его характеристическое свойство. Способы задания. Привести примеры.

Множество состоит из элементов множества, обладающих каким-либо характеристическим свойством.

Характеристическое свойство множества – например, множество четырёхугольников с равными сторонами и тп.

Способы задания множеств: 1) конечное множество можно задать перечислением;

2) с помощью характеристического свойства.

2) Множества: конечные, бесконечные. Отношения включения, универсальное множество. Диаграмма Эйлера-Венна. Привести примеры.

Множество, состоящее из конечного числа элементов, называется конечным, а из бесконечного – бесконечным.

Множество А называется подмножеством В, если каждый элемент множества А является элементом множества В (АВ). Если множество А является подмножеством В и если А…В, то говорят, что множество А включено в множество В (АdВ).

Множество по отношению к своим подмножествам является универсальным. Универсальным называется множество, в которое включены все возможные множества.

Основное в диаграмме Эйлера-Вена то, что все множества отображаются замкнутыми контурами, а универсальное буквой U и всегда в виде прямоугольника.

3) Операция пересечения множеств. Доказать коммутативность и ассоциативность пересечения, дистрибутивность относительно объединения. Привести примеры.

Пересечением множеств А и В называется множество АВ, состоящее только из тех элементов, которые входят и в множество А и в множество В. С=АВ={x| xA  xB}

Коммутативность: АВ=ВА. Ассоциативность: (АВ)С=А(ВС). Дистрибутивность: А(ВС)=(АВ)(АС).

3) Операция объединения множеств. Доказать коммутативность и ассоциативность объединения, дистрибутивность пересечения относительно объединения множеств.

Объединением множеств А и В называется множество АВ, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В. С=АВ={x| xA  xB}.

Коммутативность: АВ=ВА. Ассоциативность: (АВ)С=А(ВС). Дистрибутивность:

А(ВС)=(АВ)(АС).

4) Операция разности множеств. Доказать антидистрибутивность разности относительно объединения множеств. Привести примеры.

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множеству а, но не принадлежат множеству В. С= АВ={x|xА  хВ}

С(АВ)(СА)(СВ)

5) Операция дополнения множеств. Доказать антидистрибутивность дополнения относительно пересечения множеств. Привести примеры.

Дополнением множества А называется разность между универсальным множеством и множеством А.

Дополнение (АВ)дополнение (А)дополнение (В)

6) Упорядоченная пара. Операция декартова произведения множеств. Доказать некоммутативность декартова произведения. Привести примеры.

Упорядоченной парой называется объект (а₁, а₂), который состоит из двух элементов и в, котором определено какой из них считать первым, а какой вторым.

Декартовым произведением множеств А и В называется множество АВ, состоящее из всех возможных упорядоченных пар, в которых на первом месте стоит элемент множества А, а на втором - В. АВ={(x;y)|xA; yB}

7) Декартов квадрат множества. Понятие отношения. Привести примеры.

Декартов квадрат: А²=АА

Всякое подмножество декартового квадрата множества называется бинарным отношением.

8) Соответствие между множествами. Множества (области) определения и значений. Способы задания. Образ и прообраз элемента множества. Привести примеры.

Соответствием между множествами А и В называется любое подмножество их декартова произведения.

Множество первых координат упорядоченных пар, принадлежащих соответствию S, называется областью определения, а множество вторых – областью значения.

Способы задания:1)граф, 2)перечисление S={(a,b); (a_n,b_n)}, 3)S=AB

Полным образом элемента аА, называется множество всех элементов bВ, для которых выполняется соответствие aSb. Полным прообразом элемента bВ, называется множество всех элементов аА, для которых выполняется соответствие aSb.

9) Одно-однозначные, одно-многозначные, много-однозначные, много-многозначные соответствия. Привести примеры.

Соответствие называется одно-однозначным, если единственному элементу множества А ставится в соответствие единственный элемент множества В.

И т. д. и т. п.

10) Функциональное соответствие. Область определения и множество значений. Привести примеры.

Соответствие f между элементами множества x и y называется функциональным, если каждому элементу множества х соответствует не более одного элемента множества y.

Множество всех первых координат упорядоченной парой называется областью определения функции, а множество всех вторых координат – областью значения.

11) Взаимно обратные соответствия. Свойства их графиков. Привести примеры.

Соответствии, относящие каждому yE(f) единственное значение x₀D(f), называется обратной.

Графики двух взаимообратных функций симметричны относительно биссектрисы первого и третьего координатных углов. (Доказывается через квадрат).

2.Общие свойства функций.

12) Действительная функция одного действительного переменного. Способы задания. Монотонность, ограниченность, чётность, нечётность, периодичность. Понятие сложной функции. Привести примеры.

Действительная функция одного действительного переменного – это соответствие, относящее каждому значению переменного не более одного значения функции.

Способы задания: 1) неявный вид (2х-у+5=0)

2) явный вид (у=2х+5)

3) параметрический (система: х=g(t); y=f(t))

4) кусочное

Функция называется монотонной, если она является неубывающей, невозрастающей. И строгомонотонной, если она является или возрастающей, или убывающей.

Функция называется ограниченной сверху, если существует такое число М, что для всех значений аргумента из области определения функции справедливо: f(x)М. Функция называется ограниченной снизу, если существует такое число М, что для всех значений аргумента из области определения функции справедливо: f(x)М.

Функция называется четной, если её область определения симметрична относительно нуля и f(x)=f(-x).

Функция называется нечетно, если её область определения симметрична относительно нуля и f(x)=-f(-x).

Функция называется периодичной с периодом Т, если для любого х из области определения функции справедливо: f(x+T)=f(x-T)

Соответствие, относящее к каждому у₀E(f) единственное x₀D(f), называется обратной функцией x=f^-1(y) по отношению к функции y=f(x).

13) Обратная функция. Необходимое и достаточное условие обратимости. Доказать признак обратимости функции.

Достаточным (признак) условием существования обратной функции является строгая монотонность, а необходимым одно-однозначность соответствия.

14) Доказать теорему о графиках взаимно-обратных функций. Отыскание обратных для алгебраических и трансцендентных. Привести примеры.

Трансцендентные функции - это функции образованные неалгебраическими действиями (sin, cos).

15) Чётные и нечётные функции. Доказать теоремы об их графиках. Доказать арифметические теоремы об указанных функциях. Привести примеры.

Функция называется четной, если её область определения симметрична относительно нуля и f(x)=f(-x).

Функция называется нечетно, если её область определения симметрична относительно нуля и f(x)=-f(-x).

Теоремы о сложении, вычитании, умножении чётных, нечётных функций. (Доказывается через определение)

График чётной функции симметричен относительно оси координат (оу). (Доказывается через определение)

График нечётной функции симметричен относительно начала координат. (Доказывается через определение)

16) Периодические функции. Основной период. Доказать теорему о связи периода функции у=f(kx) с периодом функции y=f(x). Привести примеры.

Функция f(x) называется периодической с периодом Т, если выполняется равенство f(x-t)=f(x+t).

Наименьший положительный период функции называется основным.

Если Т является основным периодом функции f(х), то Т\k, где k 0, является периодом функции f(kх).

Док-во:

f(x)=f(x+t) (1)

F(kx)=f(k(x+P)) (2)

если х=kx, то (1): F(kx)=f(kx+t) левые части (1) и (2) равны, значит равны и правые:

f(kx+T)=F(k(x+P))

kx+T= k(x+P)

P=T/k

ч.т.д.

17) Периодические функции. Доказать арифметические теоремы о периодических функциях. Доказать теорему о периодичности сложной функции от периодической функции. Привести примеры.

Функция f(x) называется периодической с периодом Т, если выполняется равенство f(x-t)=f(x+t).

Если функции f(x) и g(x) периодические с периодами Т и Р соответственно, то периодом алгебраической суммы, разности, произведения и частного этих функций является общим кратным периодов Т и Р. (Доказывается банальной подстановкой, учитывая, что каждый период функции кратен её основному).

Периодом сложной функции от периодической является период функции-аргумента. (Доказывается подстановкой).

3.Числовые последовательности и пределы.

18) Модуль числа. Доказать неравенство о модуле суммы. Доказать неравенство о модуле разности. Доказать теорему о модуле произведения и частного двух чисел.

Модулем числа х называется такое число, которое равно х, если х больше или равно нуля, и равно –х, если х меньше нуля.

<= Доказывается это всё перебором

x|+|y||x+y|

|x|-|y||x+y|

|xy|=|x||y|

|1\x|=1\|x|

19) Арифметическая прогрессия, свойства. Вывести формулу общего члена и суммы первых n-членов прогрессии.

Арифметическая прогрессия – это такая числовая последовательность, для каждого члена которой справедливо равенство: a_n=a_n_-1+d, где d это разность.

Любой элемент прогрессии равен среднему арифметическому двух своих равноудалённых соседей.

20) Геометрическая прогрессия, свойства. Вывести формулу общего члена и суммы первых n-членов прогрессии.

Геометрическая прогрессия – это такая числовая последовательность, для каждого члена которой справедливо равенство: a_n=a_n_-1*q, где q это знаменатель.

Любой элемент прогрессии равен среднему геометрическому двух своих равноудалённых соседей.

21) Предел бесконечной последовательности, геометрическая интерпретация. Доказать теорему о единственности предела последовательности.

Lim x_n=a, если для любого >0 существует такое N₀ и зависящего от , такое что для любого n N₀ выполняется равенство |x_n-a|< 

Геометрический смысл это -окружность вне которой находится конечное число элементов последовательности.

Последовательность не может иметь более одного предела. (Доказывается от противного, предположим, что 2 предела существуют и их -окружности не пересекаются – далее противоречие определению).

22) Бесконечно малая последовательность. Доказать теорему о последовательности, её пределе и бесконечно малой последовательности. Доказать теорему о произведении бесконечно малой последовательности на ограниченную последовательность.

Последовательность a_n называется бесконечно малой, если её предел равен нулю.

Для того что бы число а являлось пределом последовательности a_n необходимо и достаточно чтобы последовательность {a_n-a} была бесконечно малой.

Произведение ограниченной и бесконечно малой последовательностей, так же является бесконечно малой последовательностью.

23) Доказать арифметические теоремы о пределах сходящихся последовательностей:

-о пределе суммы двух сходящихся последовательностей

-о пределе произведения двух сходящихся последовательностей

-о пределе отношения двух сходящихся последовательностей

Предел суммы равен сумме пределов.

Предел произведения равен произведению пределов.

Предел отношения равен отношению пределов.

24) Бесконечно большая последовательность. Доказать теорему о связи бесконечно малой и бесконечно большой последовательностей.

Последовательность a_n называется бесконечно большой, если для любого числа А найдётся такое N, что для любого n>N будет выполняться неравенство |a_n|<A.

Если последовательность а_n является бесконечно большой, то последовательность 1/a_n является бесконечно малой.

25) Доказать теорему о переходе к пределу в неравенстве для двух последовательностей.

Если для всех значений N, кроме, может быть, конечного числа, выполняется неравенство a_n<b_n, при этом пределы этих последовательностей равны a и b соответственно, то a<b.

26) Доказать теорему о «зажатой» последовательности.

Если даны три последовательности a_n, b_n и c_nпричём lim a_n=lim c_n=b и для всх n выполняется неравенство a_nb_nc_n то и последовательность b_n тоже имеет предел, равный b.

27) Необходимое и достаточное условие существования предела последовательности.

Ограниченность и монотонность.

28) Доказать второй замечательный предел для последовательности.

29) Вывести формулу сумм членов бесконечно убывающей геометрической прогрессии.

4.Предел функции.

30) Дать определение предела функции по Коши и по Гейне. Доказать эквивалентность этих определений.

По Гейне: Число А называется пределом функции в точке «а», если для любой последовательности значений аргумента {x_n} такой, что lim x_n=a, последовательность соответствующих значений функции {f(x_n)} имеет один и тот же предел, равный А.

По Коши: число А называется пределом функции f(x) в точке x=a, если для любого >0 существует такое >0, что если удовлетворяется неравенство |x-a|<, то удовлетворяется неравенство |f(x)-A|<.

Докажем их равносильность:

Если функция имеет предел по Гейне, то найдётся такой номер N, что при n>N будут выполняться оба неравенства |x-a|<, |f(x)-A|<, а это значит, что существует предел и по Коши. Если функция имеет предел по Коши, то взяв последовательность значений аргумента такую, что при n>N будет выполняться неравенство |x_n-a|<, убедимся, что в этом случае (при n>N) будет выполняться неравенство |f(x₀)-A|<g, а это значит, что функция имеет предел и по Гейне.

31) Бесконечно малая функция. Доказать теорему о функции, её пределе и бесконечно малой функции.

Бесконечно малая функция – это функция, предел которой равен нулю.

Число А является пределом функции y=f(x) при xa тогда и только тогда, когда эту функцию можно представить в виде суммы числа А и бесконечно малой функции.

Доказательство:

Пусть f(x)=A+(x), где (x)-бесконечно малая функция при xa. Это значит, что каково бы ни было g>0, найдётся такое M>0, что если |x_n-a|<, то |(x)|< g и |f(x)-A|<, т.е число А является пределом функции.

32) Доказать арифметические теоремы о пределах функций:

- о пределе суммы и разности двух функций, имеющих пределы;

- о пределе произведения бесконечно малой функции на ограниченную функцию;

- о пределе произведения двух функций, имеющих пределы;

- о пределе частного двух функций, имеющих пределы.

Предел суммы двух функций равен сумме пределов этих функций, если эти пределы существуют.

Произведение бесконечно малой функции на ограниченную является бесконечно малой функцией.

Предел произведения двух функций, имеющих пределы равен произведению этих пределов.

Предел частного двух функций, имеющих предел, равен отношению пределов этих функций.

33) Доказать теорему о связи бесконечно большой и бесконечно малой функций.

Если f(x) – бесконечно большая функция при xa, то 1/f(x) – бесконечно малая.

34) Односторонние пределы. Доказать теорему о связи существования предела функции в точке с существованием односторонних пределов функции.

Число А называется пределом функции f(x) в точке х=а, если каково бы ни было g>0, найдётся такое M>0, что для любого х, удовлетворяющего условию a<x<a+M выполняется неравенство |f(x)-A|<g.

Аналогично определение левого предела функции, только в этом случае x должен удовлетворять условию a-M<x<a.

Функция f(x) имеет предел в точке х=а тогда и только тогда, когда в этой точке существуют правый и левый пределы, и они раны между собой. Общее значение этих пределов и является пределом функции f(x) в точке х=а.

35) Доказать теоремы о единственности предела в точке и о предельном переходе в равенстве двух функций.

Функция f(x) в точке х=а может иметь только один предел.

Доказательство:

Докажем, что при xa функция имеет два различных предела. Обозначим их А и В, причём АВ. Для определённости будем считать, что В>A. Это означает, что если взять g<(B-A)/2, то будет выполняться неравенство A+g<B- g, и тогда g-окрестности точек А и В не будут пересекаться. Однако по определению предела должно существовать такое M, что если |x-a|<M, то |f(x)-A|<g и |f(x)-В|<g, а это невозможно. Мы получили противоречие, а значит теорема доказана.

Следствие: Если две функции, f(x) и g(x), равны на некотором множества D, принадлежащем их областям определения, то и их пределы в любой точке аD равны.

36) Доказать теорему о предельном переходе в неравенстве для двух функций.

Если функции f(x) и g(x) при xàa имеют пределы и f(x)< g(x), то предел f(x) меньше либо равен пределу g(x).

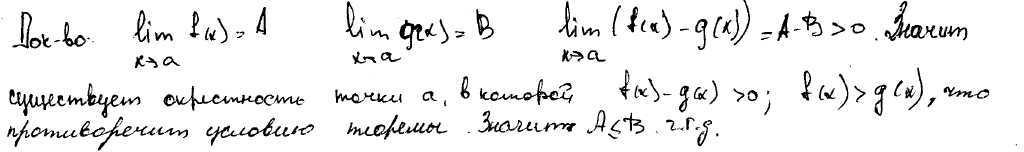
37) Доказать теорему о «зажатой» функции.

Если тир функции f(x), g(x) и h(x) определены в одной и той же окрестности точки а: |x-a|<M, причём f(x)g(x)h(x) и пределы f(x) и h(x) равны А, то и предел g(x) равен А.

38) Доказать первый замечательный предел.

39) Доказать необходимое условие и сформулировать признак существования предела в точке.

Существование и равенство односторонних пределов в этой точке.

40) Доказать теорему о пределе сложной функции.

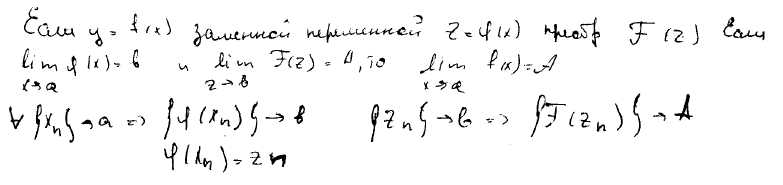
41) Сравнение бесконечно малых функций. Эквивалентность бесконечно малых функций. Привести примеры эквивалентных бесконечно малых функций: ln(1+x)x при x0; e^x -1+x при xà0; cos x -x²/2 при xà0; (1+x)^a -1+ax при xà0.

Бесконечно малые функции h(x) и g(x) при xàa называются величинами одного порядка малости, если существует lim_x_à_a h(x)/ g(x)=A0.

Бесконечно малая функция h(x) называется величиной более высокого порядка малости по сравнению с бесконечно малой g(x) при xàa, если lim_x_à_a h(x)/ g(x)=0.

Бесконечно малая функция h(x) называется величиной более низкого порядка малости по сравнению с бесконечно малой g(x) при xàa, если lim_x_à_a h(x)/ g(x)= 4.

Бесконечно малые функции называются несравнимыми, если предел их отношения не существует.

Бесконечно малые функции называются эквивалентными при xàa, если предел их отношения равен 1.

5.Непрерывность функции в точке.

42) Дать определение непрерывности функции в точке. Доказать арифметические теоремы о непрерывных функциях. Непрерывность суперпозиции непрерывных функций.

Функция f(x) определена в некоторой окрестности точки х₀, если lim _x_à_х0 =f(x₀)

Если функции f(x) и g(x) непрерывны в точке х₀, то так же непрерывны в этой точке функции f(x)+ g(x), f(x)/ g(x) при g(x)…0, f(x) ^. g(x).

Если f(x) и g(x) – непрерывные функции, то функция f(g(x)), так же непрерывна.

43) дать второе определение непрерывности функции в точке. Доказать эквивалентность этих определений.

Функция f(x) непрерывна в точке х₀, если приращение функции в этой точке является бесконечно малой величиной при приращении аргумента, стремящемся к нулю.

44) Дать классификацию точек разрыва (первого и второго рода).

Тип разрыва, когда в точке х₀ имеются (конечные) правый и левый переделы функции, называют разрывом первого рода. В противном случае говорят, что х₀– разрыв второго рода.

6.Производная функции в точке.

45) Производная, её геометрический смысл. Вывести формулы касательной и нормали к графику функции в точке.

Производной данной функции в данной точке называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю.

Геометрический смысл производной в точке, это тангенс угла наклона касательной к этой точке.

46) Левая и правая производные функции в точке.

47) Бесконечная производная в точке.

48) Доказать арифметические теоремы о производных.

49), 50), 51), 53) Вывести формулу для производной степенной и показательной функций. Вывести формулу для производной логарифмической функции. Вывести производные синуса, косинуса, тангенса, и котангенса. Вывести формулу для производной функции арксинус, арккосинус, арктангенс, арккотангенс.

52) Доказать теорему о производной обратной функции.

Пусть функция f(x) имеет обратную функцию и конечную, отличную от нуля производную. Тогда для обратной функции существует производная, равная 1/f’(x).

54) Доказать теорему о производной сложной функции.

Производная сложной функции равна производной функции по промежуточному аргументу, умноженной на производную промежуточного аргумента.

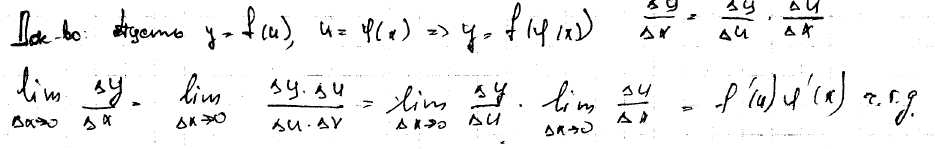
7.Основные теоремы дифференциального исчисления.

55) Дать определения максимума и минимума в точке. Доказать необходимое условие экстремума функции в точке (теорему Ферма). Дать определения стационарных и критических точек.

Точка х₀ называется точкой локального минимума (максимума) для функции y=f(x) если найдётся такая окрестность этой точки (х₀-, х₀+M), что для любого х(х₀-, х₀+M) f(x)f(х₀) (f(x)f(х₀))

Теорема Ферма: Если функция имеет в точке экстремума конечную производную, то эта производная равна нулю.

Стационарные точки – это точки в которых вторая производная равна нулю.

Критические точки это точки из области определения функции, в которых производная равна нулю или не существует.

56) Доказать теорему Роля и теорему Лагранжа о конечном приращении функции. Рассказать о геометрической интерпретации этих теорем.

Теорема Роля: Если функция y=f(x) непрерывна на отрезке [a, b], имеет конечную производную в точке этого отрезка и принимает на концах отрезка равные значения, то между а и b существует хотя бы одна точка с, в которой f’(с)=0.

Теорема Лагранжа: если функция y=f(x) непрерывна на отрезке [a, b] и имеет конечную производную в каждой точке, принадлежащей этому отрезку, то между а и b найдется, по крайней мере, одна точка с, в которой f’(с)=(f(b)-f(a))/(b-a).

Геометрический смысл теоремы Лагранжа заключается в том, что если точки (a, f(a)) и (b, f(b)) на графике функции соединить хордой, то на отрезке [a, b] будет лежать точка с, в которой касательная к графику функции будет параллельна хорде. Что бы доказать это достаточно вычислить угловой коэффициент хорды.

Если в формулу Лагранжа вместо а и b подставить x и x+)x, то получим

f(x+)x)-f(x)=f’(x+)x) )x, где [0, 1]

от куда f(x+)x)=f(x)+f’(x+)x) )x

эта формула называется формулой конечных пределов и используется для приближённых вычислений.

58) Выпуклость вниз и выпуклость вверх графика функции в точке. Точки перегиба графика функции.

График имеет выпуклость вверх, если касательная к графику в этой точке находится над графиком. График имеет выпуклость вниз, если касательная в этой точке находится под графиком.

В том случает, если производная в точке равна нулю, а экстремума в этой точке нет, на графике функции будет точка перегиба (точка, в которой касательная к кривой пересекает кривую).

57) Доказать достаточные условия максимума и минимума функции в точке.

Пусть функция y=f(x) непрерывна в точке х₀ и имеет производную в некоторой окрестности (х₀-M, х₀+M) этой точки, тогда:

Если производная в левой полуплоскости точки х₀ положительна, а в правой отрицательна, то х₀ – точка максимума.
Если производная в левой полуплоскости точки х₀ отрицательна, а в правой положительна, то х₀ – точка минимума.

58) Наибольшее и наименьшее значение функции на числовом множестве.

Если функция на отрезке [a, b] непрерывна и внутри отрезка дифференцируема, то внутри отрезка она имеет наибольшее и наименьшее значение.

61) Сформулировать основные положения схемы исследования и построения графика функции.

1. Найти область определения функции, её точки разрыва и вертикальные асимптоты.

2. Установить такие свойства функции, как чётность, нечётность, периодичность.

3. Найти точки пересечения графика с осями координат, интервалы знакопостоянства, выяснить поведение функции на концах промежутков области определения.

4. Найти наклонные или горизонтальные асимптоты.

5. Найти точки экстремума, промежутки возрастания и убывания функции.

6. Если требуется, найти точки перегиба и интервалы выпуклости и вогнутости функции.

7. Свести результаты исследования в таблицу и построить график.

Алгебра.

8.Линейная функция.

62) Доказать свойства линейной функции и построить её график. Привести примеры. Вывести уравнение прямой, проходящей через две заданные точки.

Коэффициент k обозначает тангенс угла наклона, а свободный коэффициент точка пересечения с осью оу.

(x-x_a)\(x_b-x_a)=(y-y_a)\(y_b-y_a)(выводится через систему)

63) Доказать условие параллельности и перпендикулярности прямых. Вывести формулу для тангенса угла между прямыми.

k₁=k₂ – прямые параллельны.

k₁k₂=-1 – прямые перпендикулярны

tgφ=| (k₁-k₂)\ (1+k₁k₂)|

9.Квадратный трёхчлен.

59) Выделение полного квадрата. Привести примеры. Вывести формулы для его корней. Дискриминант. Доказать прямую и обратную теоремы Виета.

Выделение полного квадрата:

и получим канонический вид квадратного трёхчлена.

Формулы его корней:

Выражение вида b²-4ac принято называть дискриминантом.

Прямая теорема Виета:

Обратная теорема Виета:

60) Доказать теорему о разложении на линейные множители квадратного трёхчлена. Построение графика квадратного трёхчлена по его коэффициентам.

Если х₁ и х₂ – корни квадратного уравнения, то квадратный трёхчлен разлагается на линейные множители вида: Ax²+Bx+C=A(x-x₁)(x-x₂)

61) Доказать необходимое и достаточное условие того, что данное число  меньше корней квадратного уравнения.

- Доказать необходимое и достаточное условие того, что данное число  располагается между корнями квадратного уравнения.

- Доказать необходимое и достаточное условие того, что данное число  больше корней квадратного уравнения.

- Доказать необходимое и достаточное условие того, что данное число  совпадает с меньшим (большим) корнем квадратного уравнения.

f()\А<0

система: f()\А>0; х_в->0 (больше)

система: f()\А>0; х_в-<0 (меньше)

система: f()\А=0; х_в->0 (совпадает с большим)

система: f(l)\А=0; х_в-l<0 (совпадает с меньшим)

Доказывается банально через рисунки (4 параболы). И ко всем условиям надо не забывать дискриминант больше либо равен нуля.

10.Комплексные числа.

62) Комплексная плоскость. Действия над комплексными числами в декартовой форме.

С помощью базисных векторов задаются целая и мнимая части комплексного числа.

Суммой двух комплексных чисел z₁ и z₂ называют комплексное число z=(x₁+x₂)+i(y₁+y₂). Другими словами для нахождения суммы двух комплексных чисел необходимо сложить их действительные и мнимые части. Сумма двух комплексно-сопряжённых чисел есть всегда действительное число равное их удвоенной действительной части.

Для нахождения разности комплексных чисел необходимо вычесть отдельно их действительные и мнимые части.

Произведением двух комплексных чисел z₁ и z₂ называют комплексное число

68) Комплексно-сопряжённые числа. Теоремы о сопряжённости суммы и произведения комплексно-сопряжённых чисел.

Два комплексных числа называют комплексно сопряженными, если они имеют одну и ту же действительную часть и взаимно противоположные мнимые части.

Число, сопряжённое с суммой комплексных чисел есть сумма чисел сопряжённых слагаемым.

Число, сопряжённое с произведением двух комплексных чисел есть произведение чисел, сопряжённых с сомножителями.

11.Теория многочленов.

69) Действия над многочленами. График многочлена. Алгоритм деления многочленов с остатком (алгоритм Евклида).

При сложении многочленов складывают коэффициенты при одинаковых степенях переменной. Для сложения многочленов существует однозначно определённая обратная операция – вычитание многочленов. При умножении многочленов перемножают каждый одночлен первого сомножителя на каждый одночлен второго, затем приводят подобные члены.

Вот так примерно выглядит график многочлена.

Алгоритм Евклида это деление столбиком.

70) Теорема Безу. Следствия.

Остаток от деления многочлена на (х-α) равен значению многочлена при х=α.

Действительно, в соответствии с алгоритмом деления с остатком многочлена произвольной степени на многочлен первой степени имеем P_n(x)=(x- α)q_n_-1(x)+R₀. Здесь остаток R₀ либо нуль, либо какое-либо число (многочлен нулевой степени), подставляя в это равенство х=α, получаем P_n(α)=( α- α)q_n_-1(α)+R₀  R₀=P_n(α)

Следствие 1: Если число α является корнем многочлена P_n(x), то этот многочлен без остатка делится на линейный двучлен (x- α)

Следствие 2: Если α₁ и α₂ различные корни многочлена P_n(x), то многочлен делится на квадратный трёхчлен ((x- α₁) (x- α₂)).

Следствие 3: Если α₁, α₂…α_k – попарно различные корни многочлена P_n(x), то этот многочлен без остатка делится на многочлен k-ой степени ((x- α₁) (x- α₂)…(x- α_k))

71) Связь между корнем многочлена и делимостью его на линейные множители. Схема Горнера.

Если число α является корнем многочлена P_n(x), то этот многочлен без остатка делится на линейный двучлен (x- α)

72) Понятие простого и кратного корней многочлена. Доказать теорему о целом и рациональном корнях многочлена с целыми коэффициентами.

Если число α является k-кратным корнем многочлена P_n(x), то α будет корнем кратности k-1 первой производной этого многочлена. Если α – простой корень многочлена P_n(x), то число α не является корнем многочлена P_n’(x).

73) Сформулировать основную теорему алгебры. Следствие о разложении многочлена n-ой степени в произведение n линейных сомножителей.

Основная теорема алгебры: всякий многочлен степени не меньше первой имеет не меньше 1-го корня.

Всякий многочлен P_n(x) не нулевой степени, с любыми числовыми коэффициентами может быть представлен в виде произведения n линейных множителей, причём единственным образом с точностью до порядка расположения.

74) Следствие о количестве корней многочлена n-ой степени.

Всякий многочлен P_n(x) не нулевой степени, с любыми коэффициентами имеет n-корней, в общем случае комплексных, при этом каждый корень подсчитывается столько раз, какова его кратность.

75) Многочлен с действительными коэффициентами. Леммы о комплексно-сопряжённых корнях и о делимости многочлена на квадратный трёхчлен с действительными коэффициентами. Следствие основной теоремы о разложении многочлена в произведение непереводимых сомножителей.

Многочлен с действительными коэффициентами – это многочлен, у которого все коэффициенты являются действительными числами.

Лемма 1: Если комплексное число α является корнем многочлена P_n(x), то и сопряженное ей число α₁ так же является корнем этого многочлена.

Лемма 2: Если α и α₁ комплексно-сопряженные корни многочлена P_n(x), то это многочлен делится нацело, то этот многочлен делится нацело на неприводимый квадратный трёхчлен с действительными коэффициентами.

12.Дробно-рациональная функция.

76) Правильная и простейшие рациональные дроби. Теорема о представлении рациональной дроби в виде суммы многочлена и правильной дроби. Алгоритм разложения правильной дроби в сумму простейших дробей.

Рациональная дробь, у которой степень числителя меньше степени знаменателя называется правильной.

Рациональная дробь называется простейшей, если её знаменатель является неприводимым многочленом, а степень числителя равна 0 или 1 (0, если в знаменателе стоит бином, и 1, если – квадратный трёхчлен).

Всякая рациональная дробь представима, притом единственным образом, в виде суммы многочлена и правильной дроби.

Разложение правильной дроби в сумму простейших:

13.Степенная и показательная функция.

77) Свойства степени с натуральным показателем. Степенная функция с натуральным показателем. Её свойства и график.

Свойства степени:

График и свойства степенной функции.

78) Доказать свойства степени с целым показателем. Степенная функция с целым показателем, её свойства и график.

79) Арифметический и алгебраический корень. Показать на примере существование арифметического корня.

Корнем n-степени из числа а называется такое число n-степень которого равна а.

Арифметическим корнем из числа а называется неотрицательный корень из этого числа.

Примером арифметического корня служит график корня.

80) Степенная функция корень n-степени из х. Доказать её свойства и построить график.

81) Свойства степени с рациональным показателем. Степенная функция с рациональным показателем, доказать свойства и построить график.

82) Показательная функция, доказать свойства и построить график.

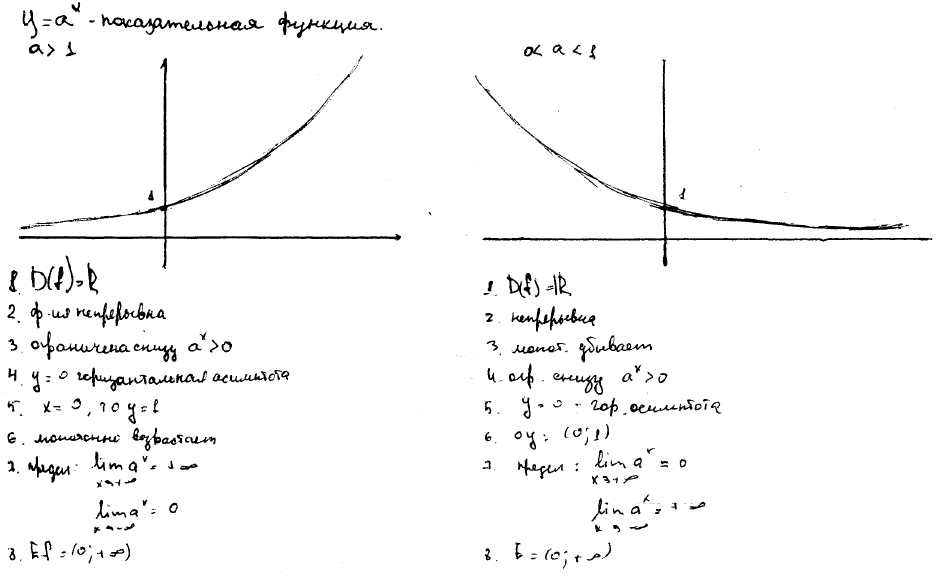
14.Логарифм числа и логарифмическа функция.

83) Логарифм числа. Основное логарифмическое тождество. Доказать теорему о логарифме произведения, частного, степени.

Показатель степени, в которую надо возвести «а», что бы получить х, называется логарифмом числа х по основанию а.

Основное логарифмическое тождество:

84) Доказать теорему о логарифме числа по основанию а^с.

85) Доказать теорему о переходе к новому основанию. Логарифмическая функция, доказать свойства, построить график.

15.Тригонометрические функции.

86) Понятие угла. Измерение углов. Направленные углы. Числовая окружность. Соответствие между множеством действительных чисел и мерой угла в радианах. Геометрическая интерпретация тригонометрических функций на координатной окружности.

Угол – это геометрическая фигура, состоящая из 2-х лучей с общим началом, и ограниченной ими плоскостью.

Направленный угол, образуется поворотом луча.

Каждому числу на числовой прямой соответствует радианная мера угла.

87) Функция синус, доказать её свойства.

88) Функция косинус, доказать её свойства.

89) Функция тангенс, доказать её свойства.

90) Функция котангенс, доказать её свойства.

91) Доказать основное тригонометрическое тождество и его следствия.

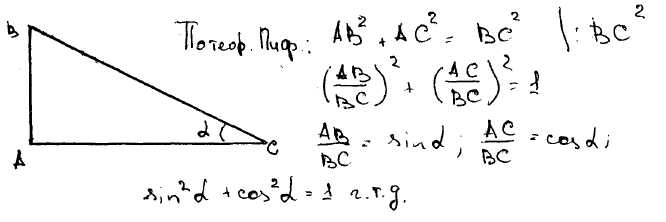
92) Доказать теоремы сложения. Вывести формулы приведения.

Доказывается через синус и косинус суммы и разности.

93) Вывести формулы двойных и половинных углов.

Выводится через синус и косинус суммы и разности.

94) Вывести формулы тригонометрических функций через тангенс половинного угла.

95) Вывести формулы преобразования суммы тригонометрических функций в произведение и наоборот.

Выводится через синус и косинус суммы и разности.

96) Вывести формулы для квадрата синуса и квадрата косинуса через косинус двойного угла.

Записать формулы двойного угла для косинуса и всё от туда выводиться.

97) Функция y=arcsin x, её свойства и график. Связь с другими обратными тригонометрическими функциями.

98) Функция y=arccos x, её свойства и график. Связь с другими обратными тригонометрическими функциями.

99) Функция y=arctn x, её свойства и график. Связь с другими обратными тригонометрическими функциями.

100) Функция y=arcctg x, её свойства и график. Связь с другими обратными тригонометрическими функциями.

101) Решение простейших тригонометрических уравнений: sin x=a; cos x=a; tg x=a; ctg x=a.

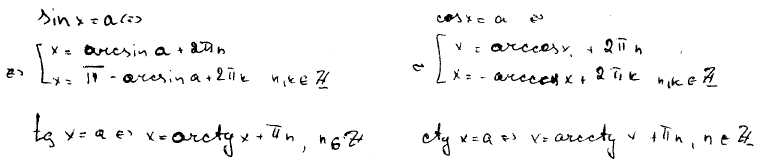
Стереометрия.

16.Аксиоматика Вейля-Рашевского.

102) Аксиоматический метод. Независимость, полнота и непротиворечивость системы аксиом.

Изучение любой теории начинается с некоторых первоначальных предложений, из которых путём рассуждений делаются дальнейшие выводы. Этот метод называется аксиоматическим.

Независимость заключается в том, что ни одна аксиома не может быть получена, как следствие других (не может быть доказана, как теорема)

Полнота заключается в том, что система аксиом должна позволять получать любое утверждение данной теории.

Непротиворечивость заключается в том, что не какие две аксиомы не должны вступать в противоречие.

103) Аксиоматика Г. Вейля - П.К.Рашевского построения геометрии. Основные группы аксиом.

Аксиоматика Г. Вейля - П.К. Рашевского: число, точка и вектор - понятия не требующее определения.

Основные понятия: точка, число и вектор.

Группы аксиом: 1) аксиомы связи между точками и векторами;

2) аксиомы умножения вектора на число;

3) аксиомы размерности;

4) аксиомы скалярного произведения.

104) Аксиомы связи. Правило треугольника сложения векторов. Доказать теорему о независимости суммы векторов от начальной точки.

АКС.1: Существует хотя бы одна точка.

АКС.2: Каждая упорядоченная пара точек определяет вектор.

АКС.3: Для каждой точка А и вектора а существует единственная точка В такая что, АВ=а.

АКС.4: Если векторы АВ и СD равны, то АС=ВD.

Т: вектор с=а+b не зависит от выбора точки приложения вектора а.

Доказывается через аксиому 4.

105) Доказать коммутативность сложения векторов. Правило параллелограмма сложения векторов.

АВ+ВС=ВС+АВ; (Для доказательства рисуется параллелограмм и одна его сторона обзывается вектором а, а другая b, далее показывается что диагональ этого параллелограмма будет вектором-суммы b+a и a+b)

Правило параллелограмма все знают.

106) Доказать ассоциативность сложения векторов и правило многоугольника сложения векторов.

(a+b)+c=a+(b+c);

107) Правило вычитания векторов. Доказать существование разности.

Для получения вектора-разности векторов а и b надо отложить эти вектора из одной точки и провести вектор из конца второго в конец первого.

108) Аксиомы умножения вектора на число. Доказать теоремы о нулевом и противоположном векторах.

АКС.1: Каждой упорядоченной паре (l;а), где l, а аV соответствует единственный вектор b=lа, называющийся произведением вектора на число.

АКС.2: Умножение вектора на 1 не изменяет вектора.

АКС.3: Умножение вектора на число дистрибутивно относительно числового множителя: l(а+b)= lа+lb

АКС.4: Умножение вектора на число дистрибутивно относительно векторного множителя.

АКС.5: Умножение вектора на число ассоциативно относительно числового множителя.

Т: Произведение нулевого вектора и любого числа равно нулю-вектору. (Для доказательства использовать, что сумма противоположных векторов равна нулю-вектору).

Т: Для любого вектора lа вектор -lа является противоположным. (Для доказательства использовать, что сумма противоположных векторов равна нулю-вектору).

109) Понятие направления. Отношения сонаправленности, противонаправленности и коллинеарности векторов.

О: Направлением называется множество векторов сонаправленных с данным вектором.

О: Ненулевые вектора а и b называются сонаправленными, если существует такое положительно число l что, а= lb.

О: Ненулевые вектора а и b называются противонаправленными, если существует такое отрицательное число l что, а=lb.

О: Сонаправленные и противонаправленные вектора называются коллинеарными или параллельными.

110) Аксиомы размерности. Два определения линейной зависимости (независимости) векторов. Доказать их эквивалентность.

АКС1: Существуют 3 линейно независимых вектора.

АКС2: Любые 4 вектора линейно зависимы.

О: Система векторов называется линейно зависимой, если существует линейная комбинация этих векторов, которая равно 0 и при этом коэффициенты перед векторами тоже были отличны от 0, если такой комбинации не существует, то система векторов называется линейно независимой.

О: Система векторов называется линейно зависимой, если один из векторов представляется линейной комбинацией остальных.

Доказывается очень просто, так как одно следует из другого.

111) Доказать теорему о системе векторов, содержащей линейно зависимую подсистему. Следствия.

Т: Если система векторов имеет линейно зависимую подсистему, то и вся система линейно зависима.

Сл.1: Если система векторов содержит 2 коллинеарных или 2 равных вектора, то она линейно зависима.

Сл.2: Если система векторов содержит нулевой вектор, то она линейно зависима.

Сл.3: Если система векторов линейно независима, то любая её подсистема линейно независима.

112) Доказать теорему о подсистеме линейно независимой системы векторов.

Если система векторов линейно независима, то любая её подсистема линейно независима. (Доказывается от противного)

17.Аффинное пространство.

113) Аффинное пространство. Базис. Размерность. Привести примеры аффинных пространств различной размерности.

Аффинным пространство называется мно-во точек и векторов, элементы которого находятся в отношениях, определённых аксиомами откладывания вектора и умножения вектора на число.

Линейно независимая система векторов называется базисом аффинного пространства, если любой вектор этого пространства может быть представлен виде линейной комбинации этих векторов.

Размерность определяется кол-вом векторов, которые могут составлять базис.

прямая, плоскость и пространство.

114) Доказать теорему о существовании и единственности разложения вектора по произвольному базису. Координаты векторов.

Т: Каждый вектор аффинного пространства может быть представлен в виде линейной комбинации базиса и при том только единственным образом.

О: Упорядоченная тройка чисел x,y,z, определяющая разложение вектора по базису называется координатами вектора в этом базисе.

115) Аффинная система координат. Радиус-вектор. Координаты точки. Доказать теорему о координатах векторов.

Совокупность произвольной точки (начала координат) и векторов, е₁, е₂ и е₃, образующих базис называют аффинной системой координат.

Радиус-вектор точки, это вектор, отложенный из начала координат к этой точке.

Упорядоченная тройка чисел (x, y, z), являющаяся координатами радауса-вектора точки А, называется координатами точки а в этом базисе.

Т: Координаты вектора в произвольном базисе равны разности координат точки конци и начала вектора в этом базисе.

116) Доказать теорему о координатах суммы векторов.

Т: Координаты суммы двух векторов равны сумм координат этих векторов.

Доказывается сложением векторов, представленных в виде линейной комбинации базисных.

117) Аффинное пространство. Доказать теорему о координатах вектора, умноженного на число.

Т: Координаты вектора, умноженного на число, равны координатам вектора, умноженным на это число.

Вектор, представляется в виде линейной комбинации базисных векторов, а потом правая и левая часть умножаются на некое число и раскрываются скобки.

118) Доказать теорему о разложении радиус-вектора точки, делящей отрезок в данном отношении.

Доказывается через сложение векторов по правило треугольника.

119) Определение прямой. Вывести векторное уравнение прямой в аффинной системе.

Множество всех точек М, для которых векторы АМ и АВ коллинеарны, называется прямой (АВ).

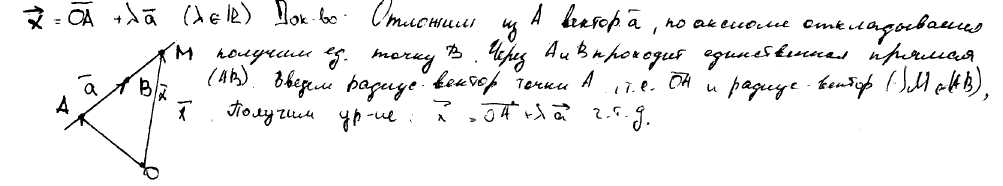
120) Определение плоскости. Доказать единственность плоскости, проходящей через три точки.

Плоскостью (АВС) называется множество точек М, для которых вектора АВ, АС и АМ линейно зависимы.

АВ и АС называются базисными векторами плоскости.

Если К, Е, Н – различные точки плоскости (АВС), не лежащие на одной прямой, то плоскость (АЕН) совпадает с плоскостью (АВС).

Следствием является то, что через три различные точки проходит только одна плоскость.

121) Базис плоскости. Вывести формулы перехода от одного базиса к другому.

Базис плоскости это два линейно независимых вектора, через которые можно выразить все векторы плоскости.

Для перехода вводится линейная зависимость.

122) Компланарные векторы. Доказать признак компланарности векторов.

Векторы называются компланарными, если они лежат в одной плоскости или параллельно данной плоскости.

Т: Для того, что бы векторы были компланарны, необходимо и достаточно, что бы они были линейно зависимы.

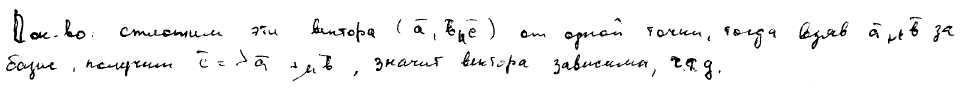
123) Доказать теорему о прямой, проходящей через две точки плоскости.

Если две различные точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.

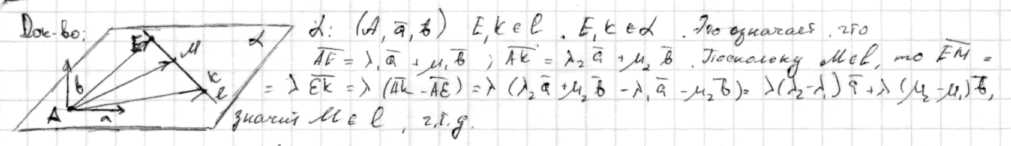
124) Взаимное расположение прямых. Доказать существование и признак параллельных прямых.

Любые две прямые имеют либо одну общую точку, либо не имеют их вообще, либо имеют бесконечное множество общих точек.

Две прямые, лежащие в одной плоскости параллельны тогда и только тогда, когда они не имеют общих точек или совпадают.

125) Взаимное расположение прямых. Доказать существование и признак пересекающихся прямых.

Для того, что бы две прямые, лежащие в одной плоскости, пересекались необходимо и достаточно, чтобы их направляющее вектора были линейно независимы.

126) Взаимное расположение прямых. Доказать признак скрещивающихся прямых.

О: Две непараллельные прямые, не имеющее общих точек, называются скрещивающимися.

Признак: Для того что бы прямые АВ и СD скрещивались необходимо и достаточно что бы векторы АВ, СD и AD образовывали базис пространства.

127) Взаимное расположение плоскостей. Доказать теорему об общих точках двух плоскостей.

Плоскости или параллельны, или пересекаются.

128) Параллельные плоскости. Признак параллельности плоскостей.

Плоскости называются параллельными, если любой вектор, параллельный одной плоскости, параллелен и другой плоскости.

Признак параллельности плоскостей: для того, чтобы плоскости были параллельны, необходимо и достаточно, чтобы они имели общий базис.

129) Теорема существования и единственности плоскости, проходящей через точку и параллельно некоторой другой плоскости.

Через каждую точку пространства проходит единственная плоскость, параллельная данной.

130) Параллельность прямой и плоскости. Признак параллельности прямой и плоскости. Доказать теорему о параллельности линий пересечения двух параллельных плоскостей третьей плоскостью.

Прямая называется параллельной плоскости, если её направляющий вектор параллелен этой плоскости.

Признак параллельности прямой и плоскости: если прямая параллельна некоторой прямой, принадлежащей плоскости , то она параллельна плоскости .

Т: Плоскость, пересекающая одну из двух параллельных плоскостей, пересекает и другую, причём линии их пересечения параллельны.

131) Доказать теорему о параллельности линии пересечения двух пересекающихся плоскостей прямой, параллельной каждой из этих плоскостей.

Попробовать доказать от противного.

132) Пересечение прямой и плоскости. Лемма о пересечении плоскости и пары
параллельных прямых.

Прямую и плоскость, которые имеют единственную общую точку, называют пересекающимися.

18.Метрнческое пространство

134) Аксиомы скалярного произведения. Длина вектора. Орты. Доказать теорему о
нормировании вектора.

АКС.1: Для любых двух векторов существует действительное число, называемое их скалярным произведением (а,b).

АКС.2: Скалярное произведение обладает свойством коммутативности.

АКС.3: Числовой множитель можно выносить за скобки скалярного произведения.

АКС.4: Скалярное произведение дистрибутивно относительно сложения векторов.

АКС.5: скалярный квадрат вектора неотрицателен.

Длиной вектора называется корень из скалярного квадрата этого вектора.

Вектор называется ортом , если его длина равна 1.

Для любого вектора существует вектор коллинеарный ему, длина которого равна 1.

135) Доказать неравенство Коши-Буняковского.

Модуль скалярного произведения векторов не превосходит произведения длин этих векторов.

136) Угол между векторами и расстояние между точками. Доказать свойства расстояния.

Косинус угла между векторами равен скалярному произведению, деленному на произведение моделей векторов.

Расстоянием называется величина вектора, соединяющего эти точки.

Свойства расстояния: 1) оно не отрицательно;

2) расстояние от А до В равно расстоянию В до А;

3) неравенство треугольника;

137) Ортогональность системы векторов. Доказать существование двух (трёх) ненулевых ортогональных векторов.

Ортогональные системы ненулевых векторов линейно независимы. (Доказывается записью 2-х скалярок, где один вектор представлен в виде линейной комбинации двух других.)

Существует 3 (2) ненулевых вектора.

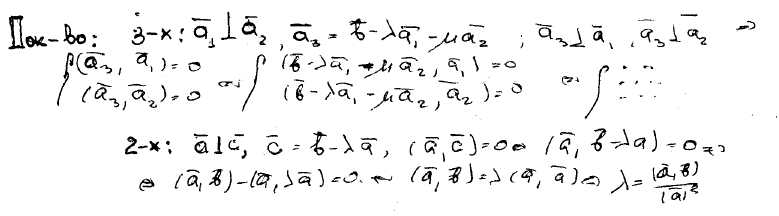
138) Доказать линейную независимость ортогональной системы векторов.

139) Проекция вектора на вектор.

Проекцией вектора а на вектор b называется скалярное произведение векторов а и b, деленное на модель вектора b.

140) Доказать теорему о проекции произведения вектора на число. Доказать теорему о проекции вектора на ось.

Т: Проекция произведения вектора на число равна произведению проекции этого вектора на число.(Выводится через определение)

Т: Проекция вектора на ось равна координатам вектора. (Выводится через определение)

141) Доказать, что в декартовой системе координаты вектора есть его проекции на оси координат.

Доказывается по определению.

142) Декартова система координат. Доказать теорему о скалярном произведении.

Декартовой системой координат называется аффинная система координат с ортонормированным базисом.

В декартовой системе координат скалярное произведение двух векторов равно сумме по парных произведений их координат.

143) Доказать теоремы о длине вектора, расстоянии между точками и угле между векторами.

Т: В декартовой системе координат длина вектора равна квадратному корню из суммы квадратов координат.

Сл.: Расстояние между точками А и В равно квадратному корню из суммы квадратов разностей соответствующих координат (причём из координат 2-й точки вычитаются координаты 1-й).

Формула для вычисления косинуса угла та же.

144) Признак перпендикулярности прямой и плоскости.

О: Прямую, пересекающую плоскость, называют перпендикулярной этой плоскости, если она перпендикулярна ко всем прямым принадлежащим этой плоскости.

Т: Что бы прямая была перпендикулярна плоскости, необходимо и достаточно, что бы она была перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

145) Теорема о плоскости, проходящей через прямую перпендикулярную другой плоскости и обратная теорема.

Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой.

146) Теорема о параллельной проекции прямой.

Прямая проектируется в прямую или точку.

147) Теорема о проекциях параллельных прямых.

Параллельные прямые проектируются либо в две параллельные прямые, лиюо в одну и туже прямую.

148) Теорема о трёх перпендикулярах.

Для того, чтобы прямая l, принадлежащая плоскости , была перпендикулярна наклонной, проведенной к этой плоскости, необходимо и достаточно, чтобы та прямая была перпендикулярна проекции наклонной на ту же плоскость.

149) Двугранные углы. Теорема о площади проекции многоугольника.

Это углы образованные двумя плоскостями.

Площадь ортогональной проекции многоугольника равна площади самого многоугольника на косинус угла между многоугольником и его проекцией.

150) Векторное произведение векторов. Доказать свойства векторного произведения.

О: Векторным произведение 2-х векторов а и b называется вектор, перпендикулярный векторам а и b, образующий с векторами а и b правый базис и равный по модулю произведению длин векторов а и b на синус угла между ними. (аb)

Св-ва: 1) (аH0)=0

2) |(aHb)|=площади параллелограмма, построенного на этих векторах.

3) (bHa)=-(aHb)

4) Числовой множитель можно вынести за знак векторного произведения: (aHb)=(aHb)

5) ((a+b) Hc)=(aHc)+(bHc)

i j k

x1 y1 z1

x2 y2 z2

6) (aHb)=

символический

определитель.

151) Векторное произведение и коллинеарности векторов. Правые (левые) тройки векторов в декартовой системе.

Векторное произведение коллинеарных векторов равняется ноль-вектору.

О: Базис, образуемый тройкой векторов, называется правым, если он обладает следующим свойством: если смотреть с конца третьего вектора на 1 и 2 векторы, то для того что бы совместить 1-й вектор со 2-ым, 1-й вектор надо повернуть против часовой стрелки на угол меньший 180⁰.

152) Смешанное произведение векторов. Доказать свойства смешанного произведения. Смешанное произведение векторов в декартовой системе координат. Доказать признак компланарности векторов.

О: Смешанным произведением трёх векторов называется скалярное произведение одного из них на векторное произведение двух других.

Св-ва: 1) Модуль смешанного произведения численно равен объёму параллелепипеда, построенного на этих векторах. (V=SоснHh)

2) Если векторы а, B, с заданы координатами в декартовой системе координат, то смешанное произведение этих векторов равно определителю третьего порядка, где каждая строка матрицы представляет собой координаты вектора.

3) Смешанное произведение трёх векторов а, b и с, положительно, если они образуют правый базис и отрицательно если – левый. Равно нулю, если векторы вообще не образуют базиса.

4) Смешанное произведение линейно зависимых векторов равно 0.

Модуль смешанного произведение в ортонормированном базисе равен определителю третьего порядка матрицы, составленной из координат векторов.

Если векторы компланарны, то их смешанное произведение равняется нулю.

153) Расстояние между геометрическими фигурами. Вывести формулу дли вычисления расстояния от точки до плоскости.

Расстояние между геометрическими фигурами – длина общего перпендикуляра.

Расстояние от точки до плоскости это длина высоты нормального треугольника.

154) Вывести формулу для вычисления расстояния между скрещивающимися прямыми.

Не знаю формулу, а принцип Шишкина объясняла.

Сайт создан в системе uCoz